Целые числа: определение и свойства

Целые числа – это основополагающие элементы математики, которые играют важную роль в различных её разделах, а также в повседневной жизни. Они включают в себя как положительные, так и отрицательные числа, а также нуль. В данной статье мы подробно рассмотрим, что такое целые числа, их свойства и применение.

Определение целых чисел

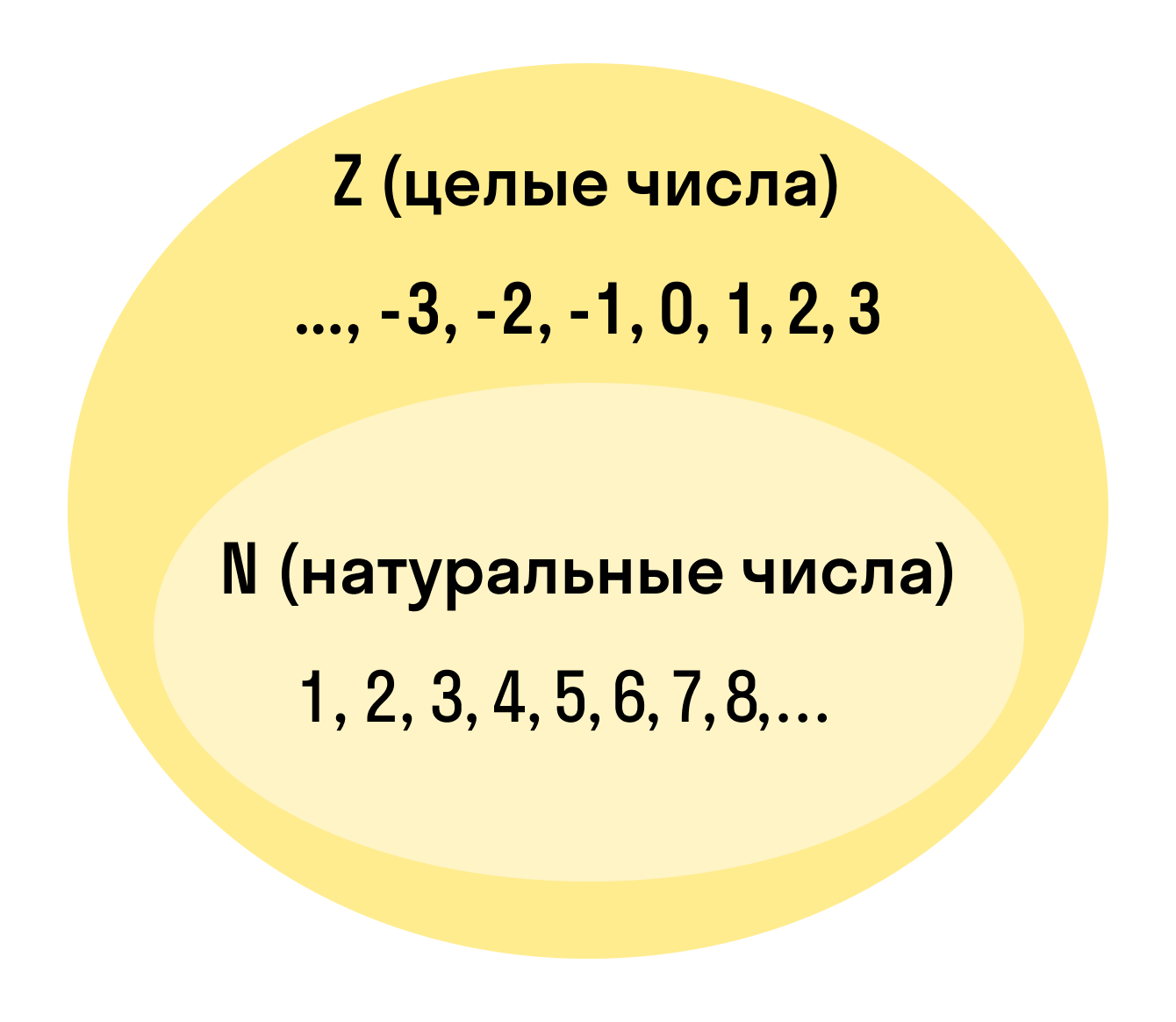
Целые числа (обозначаются $\mathbb{Z}$) – это числа, которые не имеют дробной или десятичной части. Они включают:

1. Положительные целые числа (натуральные числа): 1,2,3,4,…
2. Ноль: $0$
3. Отрицательные целые числа: −1,−2,−3,−4,…

Таким образом, множество целых чисел можно записать следующим образом: Z={…,−3,−2,−1,0,1,2,3,… }

Понимание целых чисел и их отличий от других типов чисел является важным этапом в обучении математике. Онлайн уроки математики могут значительно помочь детям и подросткам в освоении этих понятий. В этой статье мы рассмотрим, какие числа называются целыми, какие нет, и как онлайн уроки могут способствовать их пониманию.

Основные свойства целых чисел

Целые числа обладают рядом важных свойств, которые делают их фундаментальными в математике:

1. Замкнутость: Если сложить, вычесть или умножить два целых числа, результат также будет целым числом.
2. Ассоциативность: Операции сложения и умножения целых чисел ассоциативны.
3. Коммутативность: Сложение и умножение целых чисел коммутативны.
4. Существование нейтральных элементов: Для сложения нейтральным элементом является ноль, а для умножения – единица.
5. Существование противоположных элементов: Для каждого целого числа $a$ существует число $-a$, которое при сложении с $a$ даёт ноль.

Применение целых чисел

Целые числа ($\mathbb{Z}$) играют важную роль в различных областях человеческой деятельности и науки. В этой статье мы рассмотрим их применение в повседневной жизни, науке, технике и других сферах.

1. Ежедневные вычисления

Одним из наиболее очевидных применений целых чисел является их использование в повседневных вычислениях:

• Подсчет объектов: Мы используем целые числа для подсчета количества предметов, например, яблок в корзине, книг на полке, учеников в классе.
• Измерение времени: Время часто измеряется в целых числах, например, часы, минуты, дни, месяцы и годы.
• Финансовые расчеты: Целые числа используются для подсчета денег, например, количество купюр или монет, стоимость товаров и услуг в целых единицах валюты.

2. Математика и обучение

В математике целые числа являются основой для более сложных концепций:

• Арифметика: Основные арифметические операции (сложение, вычитание, умножение, деление) выполняются с целыми числами.
• Алгебра: В алгебре целые числа используются в уравнениях, неравенствах и других математических выражениях.
• Теория чисел: Целые числа изучаются в рамках теории чисел, где исследуются их свойства и отношения между ними, например, простые числа, делимость и остатки.

3. Компьютерные науки и программирование

В компьютерных науках и программировании целые числа являются неотъемлемой частью:

• Алгоритмы: Многие алгоритмы работают с целыми числами, включая сортировку, поиск и вычисление различных значений.
• Типы данных: В большинстве языков программирования существуют специальные типы данных для хранения целых чисел, такие как int в C++ или Java.
• Адресация памяти: Целые числа используются для адресации ячеек памяти в компьютере.

4. Физика и инженерия

В физических и инженерных науках целые числа применяются для измерений и расчетов:

• Измерения: В физике целые числа используются для измерения дискретных величин, например, количество атомов или квантов.
• Инженерные расчеты: В инженерии целые числа используются для проектирования и расчетов, таких как количество элементов в конструкции, целочисленные параметры в моделях и симуляциях.

5. Экономика и статистика

В экономике и статистике целые числа играют важную роль:

• Демография: В статистике используются целые числа для учета населения, количества домов, автомобилей и других объектов.
• Финансовая аналитика: В экономике целые числа применяются для анализа финансовых показателей, таких как прибыли, убытки, объемы производства и продаж.

6. Игры и спорт

Целые числа широко используются в играх и спорте:

• Счет: В спортивных играх счет ведется с использованием целых чисел для определения победителя.
• Игротехника: В настольных и видеоиграх целые числа используются для представления очков, уровней, количества жизней и других параметров.

Заключение

Целые числа представляют собой базис для изучения математики и её приложений. Их простота и фундаментальные свойства делают их незаменимыми в различных аспектах науки и жизни. Понимание целых чисел и их свойств является первым шагом на пути к более сложным математическим концепциям и достижениям.